Will I draw a Battle VIP Pass? Exploring the probabilities of the Pokémon Trading Card Game

Many card games involve chance. Regardless of how good a player or a deck is, having or not having the favor of the odds could either pave the way to an easy win or an unforgettable defeat. This rule applies to the Pokémon Trading Card Game (PTCG). Besides being cards with creatures some of us have come to love, PTCG is a complex and competitive game rich with mechanisms, options, and opportunities, where pure skill won't get you that far.

One of these cards is called Battle VIP Pass (BVP), and I'm not sure if I love or hate it. BVP is a staple card in a competitive deck. It's an Item Trainer card that lets you search your deck for up to 2 Basic Pokémon and place them onto your bench. However, it has a huge catch that's also a liability: you can only play it in your first turn.

While playing last weekend, I was in a position where I could only win if I had this card. So comes my first turn; I draw a card, and guess what? It wasn't BVP. If that wasn't enough, in game two, I was in a circumstance where I'd have loved having the card.

A Pokémon deck has 60 cards, and I run four copies of BVP. At the start of the game, each player draws seven cards and one at the beginning of each turn. So you start a match with eight cards, and yet, in two games, I got no BVP. Amid my frustration, I wanted answers; answers as to why I didn't draw any BVP. And the question to that answer is, "what's the probability of drawing a BVP in the first turn?"

I used the hypergeometric distribution function (Figure 1) to solve my calculate the probability. This distribution answers questions of the type "if I have K things in a bucket that has N things, what are my chances of getting k of these things if I draw n things from the bucket?" In my case, I want to know the probability of drawing exactly one BVP in my initial hand, considering I have four in my deck of 60 cards. To put it mathematically, and paraphrasing Wikipedia's definition, the hypergeometric distribution " describes the probability of k successes in n draws, from a finite population of size N that contains exactly K objects with that feature."

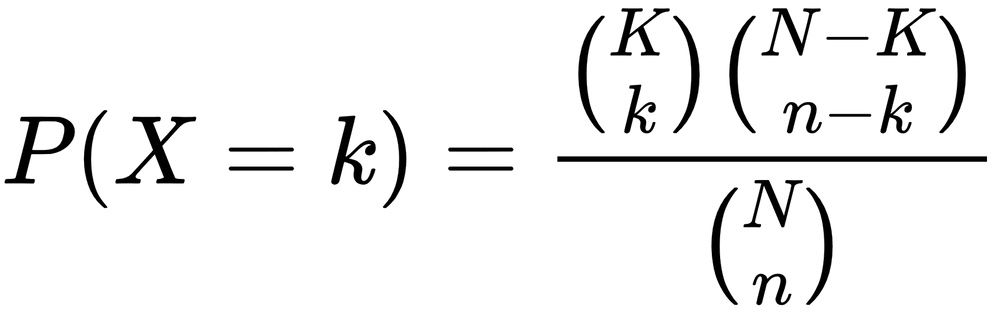
Probability of getting the card in my initial hand

Let's start with the simplest case: the probability of drawing at least one BVP in my initial hand. At the start of a match, each player draws seven cards. You want to get a BVP in this initial hand because you can only play it in your first turn. Let's find the probability using the hypergeometric distribution shown in Figure 1. But instead of just giving the number, I want to explain the process step by step.

The right-hand side of the equation is what we want to solve. The parameter K stands for how many objects of interest are in the population. Here that value is 4 because that's how many BVP I run in my deck. Next is k, the number of objects we wish to obtain. In this case, the value is 1 because I want to find at least one BVP. N is the size of the population, or the size of my Pokémon deck, which is 60. Last, there's n, the number of cards I'll draw. In this example, this value is 7 because that's how many cards you draw at the start of the game. Figure 2 presents the formula with the values plugged in. I'll skip this calculation because it involves several steps and huge numbers. If you're curious, Google "binomial coefficient," which is the name of those vertical parentheses with numbers. Meanwhile, you can see my scribbles in Figure 3.

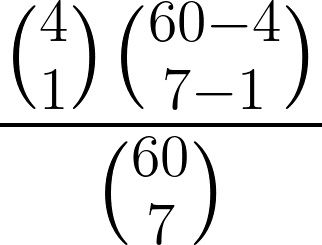
The probability of drawing at least one BVP in my initial hand is 33.63%. I thought the chances were lower due to how badly this card has treated me—but I probably forget all the times I won thanks to it, so I won't complain that much.

My deck has four BVP and not one, and ideally, I'd prefer to draw two BVP to start the match with at least four Pokémon on my bench. So, what's the probability of this event? Instead of using a calculator and my brain to solve it, I'll now write a small computer script using the Python programming language to calculate the probability of drawing two and also zero, three, and four Battle VIP Pass. I'll share the script below for those who might find it handy.

from scipy.stats import hypergeom
import numpy as np

# Supress scientific notation
np.set_printoptions(suppress=True)

def calculate(M, n, N):
    [M, n, N] = [M, n, N]
    rv = hypergeom(M, n, N)
    x = np.arange(0, n+1)
    return rv.pmf(x) * 100

calculate(60, 4, 7)

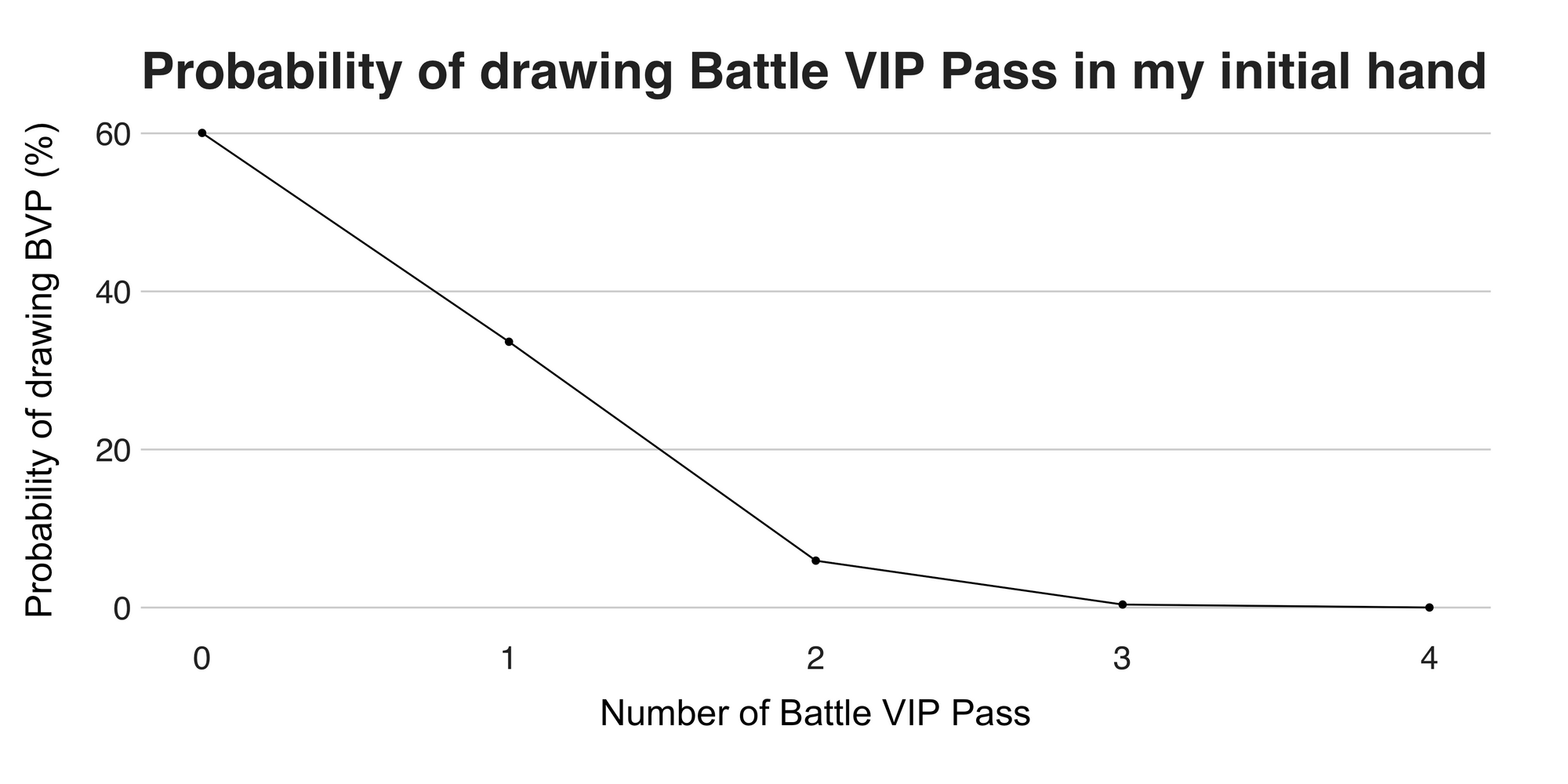
This script outputs [60.05, 33.63, 5.93, 0.38, 0.01 ], which are the probabilities of drawing zero, one, two, three, or four BVP, respectively. What's good about having all the values is that we can add them to compute the cumulative probabilities, that's it, the probabilities of getting at most or at least N cards. For example, the probability of drawing exactly two BVP is 5.93%, but that of drawing two, three, or four BVP cards is 6.32% (which is the sum of the probabilities for drawing two, three, or four BVP cards: 5.93% + 0.38% + 0.01%). The line chart below (Figure 4) visualizes the probabilities.

Drawing my first card

After drawing the initial seven cards and setting the six prizes, we start the game. Each player begins their turn by drawing a card, giving us another opportunity to get a BVP. Unlike the previous example, where we drew cards from a population of 60, now we draw from a population of 47 (60 - 7 - 6). So, supposing we didn't get any BVP in the starting hand, our new set of parameters are K = 4, k = 1, N = 47, and n = 1, which equals a probability of 8.51%.

If I start second

The drawback of starting first is that you can't play a Supporter, a type of card you can only play once in turn due to how powerful they are. Of these Supporter cards, there's one I play, and it's called Irida. This Trainer card allows the player to search in its deck for any Water Pokémon and Item card. BVP is an Item, so I could grab one off Irida and increase my chances of playing one in my first turn.

The final scenario I want to cover involves starting second, not having drawn a BVP or Irida in my initial hand, and drawing my turn's card. In this case, I want this drawn card to be a BVP or an Irida, allowing me to search for a BVP. Therefore, my new goal is to get one of these eight cards (K=8), not one of four. The probability of this happening is 17.02%, giving me an extra opportunity of seeing this acclaimed card early in the game.

Recap

Luck influences the Pokémon Trading Card Game. You could be playing the perfect game, knowing you're one turn away from victory until your opponent draws that one card that turns the match in its favor. This article focused on a single card that could decide the outcome of a game as early as the first turn. The card in question is Battle VIP Pass, which lets you fill up your bench with Pokémon only during your first turn.

Using the hypergeometric distribution, I calculated the probability of drawing a BVP in three different scenarios: drawing it in your initial hand, the first draw, or the first turn, supposing you have Irida in your deck. In the first scenario, the probability of drawing BVP in your initial hand is 33.63%. Scenario number two, which I call the fallback option, has a chance of 8.51%. Last, there's a convoluted scenario involving Irida, a card whose effect lets you search for a BVP and increases the odds of using it to 17.02%, but only if you're willing to go second.

There are hundreds of scenarios I didn't cover. They include using cards that let you draw extra cards, others that let you search for cards, and cards that let you replace your hand with the one atop your deck. What will this card be? Only the numbers know. For now, I'll cross my fingers and hope for a desirable outcome.

PS: Shout-out to Austin's Pokémon TCG community.